Hallo Stephan,
ein guter Punkt:
773H hat geschrieben: ↑Fr Jun 07, 2019 9:30 pm
Hallo. Bei der Polynomfunktion wäre es hilfreich, wenn man Infos hätte, was man machen soll, wenn die eigene Funkton von der idealen Form a + xa1 + a2x2 + a3x3 ... abweicht.
Will sagen: was mache ich, wenn ich z.B. die Formel P0=P/(1-h/44330) hoch 5.255 eingeben möchte ...
Dann möchte ich mal an diesem Beispiel zeigen, wie man hier vorgehen kann.
Mit der Basisfunktion "Ratio" haben wir schon die Möglichkeit den Quotienten A/B zu berechen.
In unserem Fall ist A der Druck (P), also brauchen wir noch eine Möglichkeit das B, den Korrekturterm (1-h/44330)
5.255, zu berechnen.
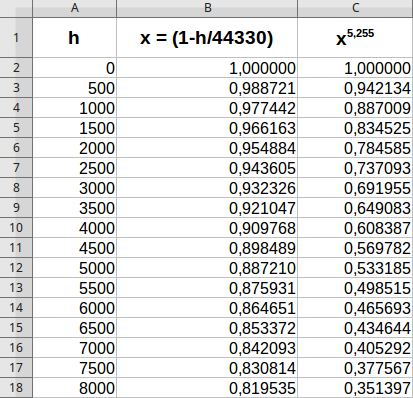
Ich will das über die Polynomfunktion machen und erstelle mir in EXEL oder LibreOffice Calc eine Wertetabelle für den gewünschten Bereich:
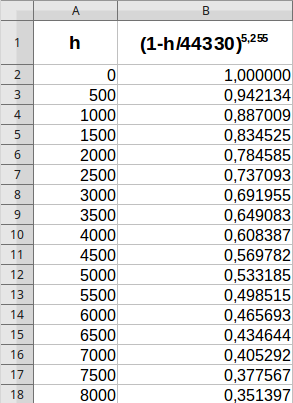
Dann gehe ich auf eine WEB-Page mit der ich mir passende Polynom-Koeffizienten berechnen lassen kann, z.B.:
https://www.arndt-bruenner.de/mathe/scripts/regr.htm, und versuche es mal mit einem Polynom 5.Grades
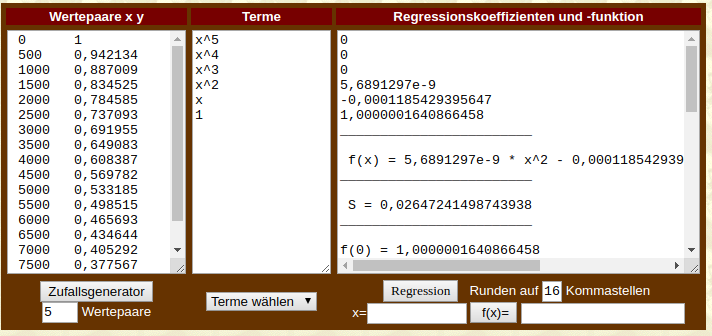
Und siehe da, es bleibt nur ein Polynom 2.Grades übrig und die Koeffizienten wähle ich mal auf sechs Stellen genau:
a
0 = 1.0
a
1 = -0.000118543
a
2 = 5.68913e-9
Damit ergibt sich folgende Custom-Logic:
Code: Alles auswählen
{
"Level": [
["$SensorWert","float",2.0],
["$Hoehe","float",550.0],
["$P_Abs","float",900.0],
["$P_Rel","float",1013.0],
["$P_Offset","float",700.0],
["$P_Gradient","float",3.2],
["$Korr_A0","float",1.0],
["$Korr_A1","float",-0.000118543],
["$Korr_A2","float",5.68913e-9],
["$H_Korr","float",0.9]
],
"Module": [
["Polynomial","$SensorWert","$P_Abs",["$P_Offset","$P_Gradient"]],
["Polynomial","$Hoehe","$H_Korr",["$Korr_A0","$Korr_A1","$Korr_A2"]],
["Ratio","$P_Abs","$P_Rel","$H_Korr"]
],
"Input": [
["SensorWert","Wert des Barometersensors","$SensorWert","c"],
["Höhe","Höhe über Meeresspiegel","$Hoehe","c"]
],
"Output": [
["P(abs)","Absoluter Druck","$P_Abs","c"],
["P(rel)","Realtiver Druck, bezogen auf Meereshöhe","$P_Rel","c"]
]
}
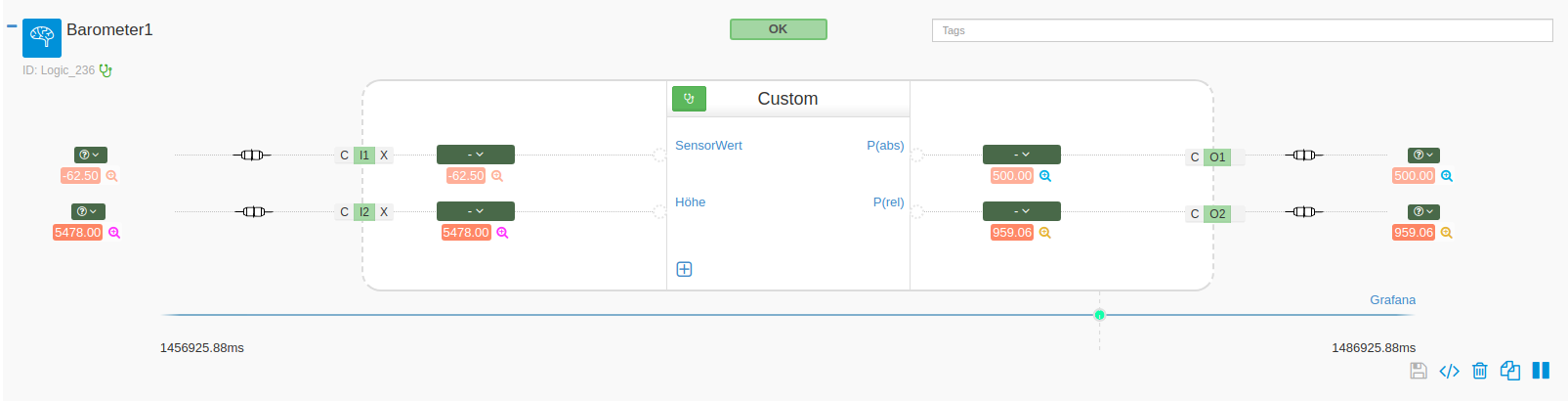
Jetzt mache ich noch eine Abschätzung, wie groß der Fehler mit dieser Näherung ist.
Dazu erweitere ich meine EXEC-Tabelle mit der Näherungsformel und berechne den relativen Fehler für den normierten Luftdruck.
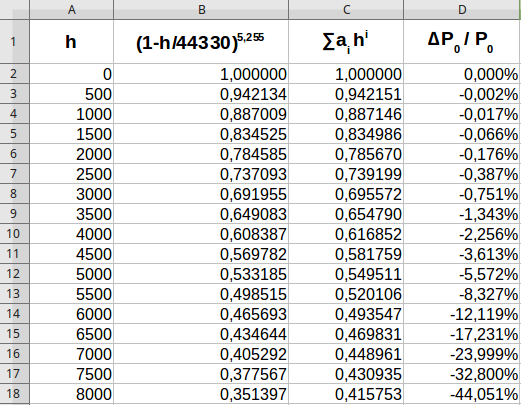
Man sieht hier, dass unter 1500m ü.NN der Fehler kleiner als 0,1% ist. Das ist vermutlich für den Großteil der Anwender ausreichend genau.
Damit aber unser Timberwolf auch noch auf Lager 4 am Mount Everest eine vernünftige Wetterprognose möglich macht, müssen wir genauer werden:
Dazu Teilen wir die Berechnung des Korrekturterms (1-h/44330)
5.255 in zwei Schritte (Polynomfunktionen) auf:
1. Schritt: x = 1-h/44330 = 1 - 0.000022558 * h
2. Schritt: Korrekturterm_B = x
5.255
Für das erste Polynom können wir die Koeffizienten direkt ablesen:
a
0 = 1.0
a
1 = -0.000022558
Für das zweite Polynom machen ich mir wieder eine Wertetabelle und lasse mir die Koeffizienten berechnen:
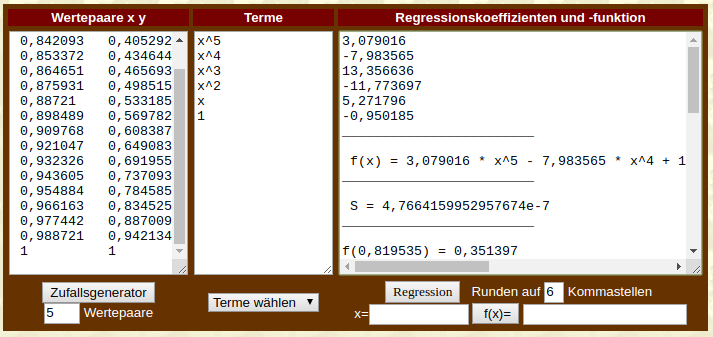
Daraus bauen wir folgende Custom-Logic:
Code: Alles auswählen
{
"Level": [
["$SensorWert","float",2.0],
["$Hoehe","float",550.0],
["$P_Abs","float",900.0],
["$P_Rel","float",1013.0],
["$P_Offset","float",700.0],
["$P_Gradient","float",3.2],
["$Korr_A0","float",1.0],
["$Korr_A1","float",-0.000022558],
["$Wert_X","float",1.0],
["$Korr_B0","float",-0.950185],
["$Korr_B1","float",5.271796],
["$Korr_B2","float",-11.773697],
["$Korr_B3","float",13.356636],
["$Korr_B4","float",-7.983565],
["$Korr_B5","float",3.079016],
["$H_Korr","float",0.9]
],
"Module": [
["Polynomial","$SensorWert","$P_Abs",["$P_Offset","$P_Gradient"]],
["Polynomial","$Hoehe","$Wert_X",["$Korr_A0","$Korr_A1"]],
["Polynomial","$Wert_X","$H_Korr",["$Korr_B0","$Korr_B1","$Korr_B2","$Korr_B3","$Korr_B4","$Korr_B5"]],
["Ratio","$P_Abs","$P_Rel","$H_Korr"]
],
"Input": [
["SensorWert","Wert des Barometersensors","$SensorWert","c"],
["Höhe","Höhe über Meeresspiegel","$Hoehe","c"]
],
"Output": [
["P(abs)","Absoluter Druck","$P_Abs","c"],
["P(rel)","Realtiver Druck, bezogen auf Meereshöhe","$P_Rel","c"]
]
}
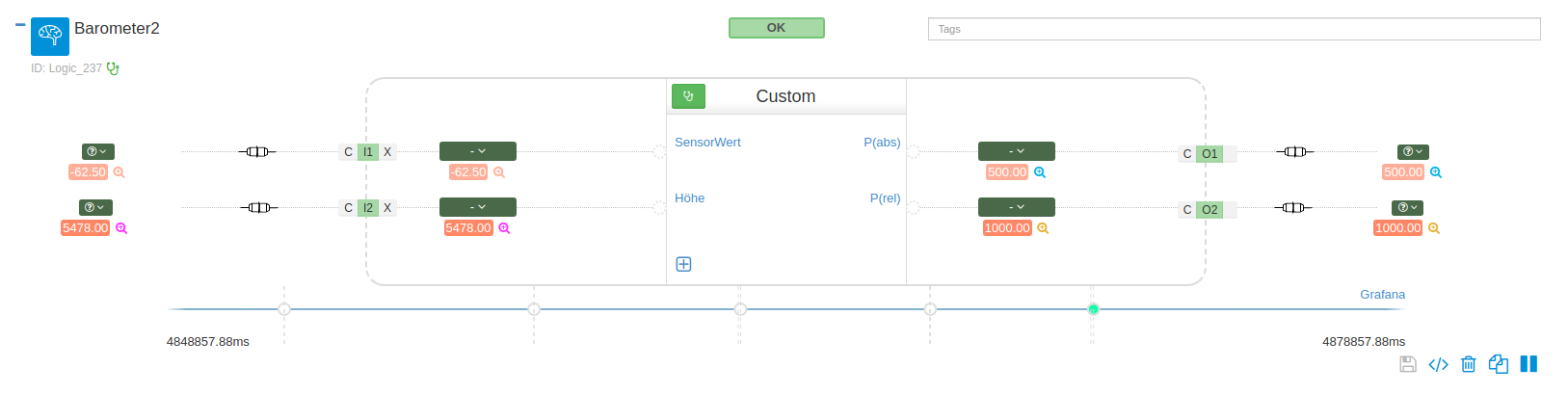
Eine erneute Fehlerberechnung des Näherungsformel ergibt:
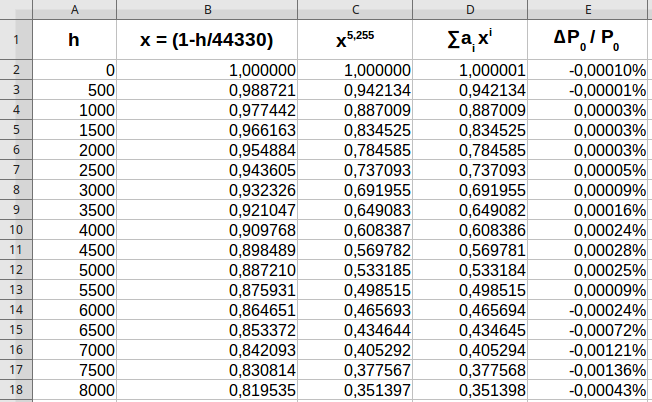
Und damit sind wir vermutlich viele, viele Größenordnungen genauer, als der Messwert des Drucksensors.







